
This book is written principally for students of precious stones and jewellers, and more particularly for diamond manufacturers and diamond cutters and polishers. The author will follow the evolution of the shape given to a cut diamond, and discuss the values of the various shapes and the reason for the discarding of the old shapes and the practically universal adoption of the brilliant.
It is a remarkable fact that, although the art of cutting a diamond has been known for more than two thousand years, it is entirely empirical, and that, though many keen contemporary minds have been directed upon the diamond, and the list of books written on that subject increases rapidly, yet nowhere can one find any mathematical work determining the best shape for that gem. The present volume's chief aim is the calculation of that shape.
The calculations have been made as simple as possible, so as not to be beyond the range of readers with a knowledge of elementary geometry, algebra, and trigonometry. Where, however, it was found that the accuracy of the results would be impaired without the introduction of more advanced mathematics, these have been used, and graphical methods have been explained as an alternative.
The results of the calculations for the form of brilliant now in use were verified by actual mensuration from well-cut brilliants. The measures of these brilliants are given at the end of the volume both in a tabulated and in a graphical form. It will be seen how strikingly near the actual measures are to the calculated ones.
The method used in the present work will be found very useful for the design of other transparent precious and semi-precious stones, although it will be found advisable in the case of stones of an agreeable colour to cut the gem somewhat thicker than the calculations warrant, so as to take full advantage of the colour. The same remark applies to diamonds of some exceptional and beautiful colour, like blue or pink, where the beauty or value of the stone increases with the depth of its colour.
It is to Indian manuscripts and early Indian literature we turn when we want to find the origin of diamond cutting, for India has always been regarded as the natural and ancient home of the diamond. It is there that they were first found : up to 1728, the date of the discovery of the Brazilian deposits, practically the whole world's supply was derived from Indian sources. They are found there in the valleys and beds of streams, and also, separated from the matrix in which they were formed, in strata of detrital matter that have since been covered by twelve to sixteen feet of earth by the accumulations of later centuries. Diamonds have existed in these deposits within the reach of man for many ages, but the knowledge of the diamond as a gem or as a crystal with exceptional qualities does not go back in India to the unfathomable antiquity which books on diamonds generally refer to. It was wholly unknown in the Vedic period, from which no specific names for precious stones are handed down at all.[1] The earliest systematic reference appears to be the Arthaçastra of Kautilya (about third century B.C.), where the author mentions six kinds of diamonds classified according to their mines, and describes them as differing in lustre and hardness. He also writes that the best diamonds should be large, regular, heavy, capable of bearing blows,[2] able to scratch metal, refractive and brilliant. In the Milinda-pañha (Questions of King Milinda) (about first century B.C.) we read that the diamond ought to be pure throughout, and that it is to be mounted together with the most costly gems. This is the first manuscript in which the diamond is classed as a gem.
Note 1. Berthold Laufer, The Diamond : a Study in Chinese and Hellenistic Folklore (Chicago, 1915).
Note 2. This legend of the indestructibility of the diamond, which reappears in many other places, and to which the test of the diamond's capacity of bearing the strongest blows was due, has caused the destruction of perhaps a very large number of fine stones. The legend was further embroidered by the remark that if the diamond had previously been placed in the fresh and still warm blood of a ram, it could then be broken, but with great difficulty. This legend was still current in Europe as late as the middle of the thirteenth century. The actual fact is that the diamond, although exceedingly hard (it is the hardest substance known), can easily be split by a light blow along a plane of crystallisation.
It is therefore permissible to estimate with a sufficient degree of accuracy that the diamond became known in India during the Buddhist period, about the fourth century B.C., and that its use as a gem dates from that period.[3]
Note 3. Laufer, loc. cit.
It is not known with certainty when and where the art of grinding or polishing diamonds originated. There is as yet no source of ancient Indian literature in which the polishing of diamonds is distinctly set forth, although the fact that diamond is used for grinding gems generally is mentioned. It is, however, likely that, where the polishing of other precious stones was accomplished in that manner, that of diamonds themselves cannot have been entirely unknown. What polishing there was must at first have been limited to the smoothing of the faces of the crystals as they were found. The first description of cut diamonds is given by Tavernier,[4] a French jeweller who travelled through India, and to whom we owe most of our knowledge of diamond cutting in India in the seventeenth century. At the time of his visit (1665) the Indians were polishing over the natural faces of the crystal, and preferred, therefore, regularly crystallised gems. They also used the knowledge they had of grinding diamonds to remove faulty places like spots, grains, or glesses. If the fault was too deep, they attempted to hide it by covering the surface under which it lay with a great number of small facets. It appears from Tavernier's writings that there were also European polishers in India at that time, and that it was to them that the larger stones were given for cutting. Whether they had learnt the art independently or from Indians and attained greater proficiency than they, or whether they were acting as instructors and teaching the Indians a new or forgotten art, is uncertain. Both views are equally likely in the present state of research upon that subject : at the time of Tavernier's visit, diamond cutting had been known in Europe for more than two centuries.
Note 4. Tavernier, Voyage en Turquie, en Perse et aux Indes (1679).
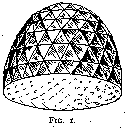
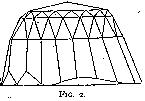
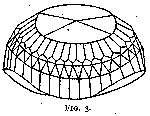
Among the several remarkable gems that Tavernier describes, the most noteworthy is the one known as the Great Mogul. This diamond was of a weight of 280 cts. and was cut as sketched in fig. 1. The polishing was the work of a Venetian, Hortensio Borgis, to whom it was given for that purpose by its owner, the Great Mogul Aurung Zeb, of Delhi. This kind of cut is characteristic of most of the large Indian stones, such as the Orlow (fig. 2), which is now the largest diamond of the Russian crown jewels and weighs 193¾ cts. The Koh-i-Noor (fig. 3), now among the British crown jewels, was of a somewhat similar shape before recutting. It weighed then 186 cts.
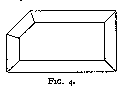
Tavernier also mentions several other types of cut which he met in India. The Great Table (fig. 4), which he saw in 1642, weighed 242 cts. Both the Great Table and the Great Mogul seem to have disappeared : it is not known what has become of them since the seventeenth century.
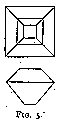
Various other shapes are described, such as point stones, thick stones, table stones (fig. 5), etc. But the chief characteristic remains : all these diamonds have been cut with one aim constantly in view -- how to polish the stone with the smallest possible loss of weight. As a consequence the polishing was generally accomplished by covering the surface of the stone with a large number of facets, and the original shape of the rough gem was, as far as possible, left unaltered.
It was mentioned before that the art of diamond polishing had already been known in Europe for several centuries when Tavernier left for India. We have as yet no certain source of information about diamond cutting in Europe before the fourteenth century. The first reference thereto mentions that diamond polishers were working in Nurnberg (Germany) in 1375, where they formed a guild of free artisans, to which admission was only granted after an apprenticeship of five to six years.[5] We do not know, however, in what shape and by what method the stones were cut.
Note 5. Jacobson's Technologisches Wörterbuch (1781).
It is in the fifteenth century that European diamond cutting begins to become more definite, more characteristic. And it is from that time that both on its technical and artistic sides progress is made at a rate, slow at first, but increasingly rapid later.
It is not difficult to find the chief reason for that change.
Up to that time, diamonds had almost exclusively been used by princes or priests. To princes they were an emblem of power and wealth -- in those days diamonds were credited with extraordinary powers : they were supposed to protect the wearer and to bring him luck. Princes also found them convenient, as they have great value for a very small weight, and could easily be carried in case of flight. Priests used them in the ornaments of temples or churches ; they have not infrequently been set as eyes in the heads of statues of Buddha.
In the fifteenth century it became the fashion for women to wear diamonds as jewels. This fashion was started by Agnes Sorel (about 1450) at the Court of Charles VII of France, and gradually spread from there to all the Courts of Europe.
This resulted in a very greatly increased demand, and gave a strong impulse to the development of diamond polishing. The production increased, more men applied their brains to the problems that arose, and, as they solved them and the result of their work grew better, the increasing attractiveness of the gem increased the demand and gave a new impulse to the art.
At the beginning of the fifteenth century a clever diamond cutter named Hermann established a factory in Paris, where his work met with success, and where the industry started developing.
In or about 1476 Lodewyk (Louis) van Berquem, a Flemish polisher of Bruges, introduced absolute symmetry in the disposition of facets, and probably also improved the process of polishing. Early authors gave credence to the statement of one of his descendants, Robert van Berquem,[6] who claims that his ancestor had invented the process of polishing the diamond by its own powder. He adds : " After having ground off redundant material from a stone by rubbing it against another one (the process known in modern practice as ' bruting ' or cutting), he collected the powder produced, by means of which he polished the diamond on a mill and certain iron wheels of his invention."
Note 6. Robert de Berquem, Les merveilles des Indes : Traité des pierres précieuses (Paris, in-4°, 1669), p. 12 : " Louis de Berquem l'un de mes ayeuls a trouvé le premier l'invention en mil quatre cent soixante-seize de les tailler avec la poudre de diamant même. Auparavant on fut contraint de les mettre en œuvre tels qu'on les rencontrait aux Indes, c'est-à-dire tout à fait bruts, sans ordre et sans grâce, sinon quelques faces an hasard, irrégulières et mal polies, tels enfin que la nature les produit. Il mit deux diamants sur le ciment et après les avoir égrisés l'un contre l'autre, il vit manifestement que par le moyen de la poudre qui en tombait et à l'aide du moulin et certaines roues de fer qu'il avait inventées, il pourrait venir à bout de les polir parfaitement, même de les tailler en telle manière qu'il voudrait. Charles devenu duc Bourgogne lui mit trois grands diamants pour les tailler avantageusement selon son adresse. Il les tailla aussitôt, l'un épais, l'autre faible et le troisième en triangle et il y réussit si bien que le duc, ravi d'une invention si surprenante, lui donna 3000 ducats de récompense."
As has already been shown, we know now that diamonds were polished at least a century before Lodewyk van Berquem lived. And as diamond is the hardest substance known, it can only be polished by its own powder. Van Berquem cannot have invented that process. He may perhaps have introduced some important improvement like the use of cast-iron polishing wheels, or possibly have discovered a more porous kind of cast iron -- one on which the diamond powder finds a better hold, and on which polishing is therefore correspondingly speedier.
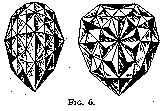
What Van Berquem probably did originate is, as already stated, rigid symmetry in the design of the cut stone. The introduction of the shape known as pendeloque or briolette is generally ascribed to him. The Sancy and the Florentine, which are both cut in this shape, have been said to have been polished by him. The Sancy (53¾ cts.) belongs now to the Maharaja of Guttiola, and the Florentine (fig. 6), which is much larger (133 1/5 cts.), is at present among the Austrian crown jewels. The history of both these gems is, however, very involved, and they may have been confused at some period or other with similar stones. That is why it is not at all certain that they were the work of Van Berquem. At any rate, they are typical of the kind of cut he introduced.
The pendeloque shape did not meet with any very wide success. It was adopted in the case of a few large stones, but was gradually abandoned, and is not used to any large extent nowadays, and then in a modified form, and only when the shape of the rough stone is especially suitable. This unpopularity was largely due to the fact that, although the loss of weight in cutting was fairly high, the play of light within the stone did not produce sufficient fire or brilliancy.
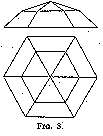
About the middle of the sixteenth century a new form of diamond was introduced. It is known as the rose or rosette, and was made in various designs and proportions (figs. 7 and 8). The rose spread rapidly and was in high vogue for about a century, as it gave a more pleasant effect than the pendeloque, and could be cut with a much smaller loss of weight. It was also found very advantageous in the polishing of flat pieces of rough or split diamond. Such material is even now frequently cut into roses, chiefly in the smaller sizes.
In the chapter upon the design of diamonds it will be shown that roses have to be made thick (somewhat thicker than in fig. 7) for the loss of light to be small, and that the flatter the rose the bigger the loss of light. It will also be seen there that the fire of a rose cannot be very high. These faults caused the rose to be superseded by the brilliant.
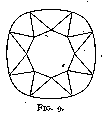
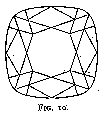
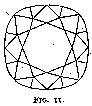
We owe the introduction of the brilliant in the middle of the seventeenth century to Cardinal Mazarin -- or at any rate to his influence. As a matter of fact, the first brilliants were known as Mazarins, and were of the design in fig. 9. They had sixteen facets, excluding the table, on the upper side. They are called double-cut brilliants. Vincent Peruzzi, a Venetian polisher, increased the number of facets from sixteen to thirty-two (fig. 10) (triple-cut brilliants), thereby increasing very much the fire and brilliancy of the cut gem, which were already in the double-cut brilliant incomparably better than in the rose. Yet diamonds of that cut, when seen nowadays, seem exceedingly dull compared to modern-cut ones. This dullness is due to their too great thickness, and to a great extent also to the difference in angle between the corner facets and the side facets, so that even if the first were polished to the correct angle (which they were not) the second would be cut too steeply and give an effect of thickness. Old-cut brilliants, as the triple-cut brilliants are generally called, were at first modified by making the size and angle of the facets more uniform (fig. 11), this bringing about a somewhat rounder stone. With the introduction of mechanical bruting or cutting (an operation distinct from polishing ; see p. 17) diamonds were made absolutely circular in plan (fig. 37). The gradual shrinking in of the corners of an old-cut brilliant necessitated a less thickly cut stone with a consequent increasing fire and life, until a point of maximum brilliancy was reached. This is the present-day brilliant.[7]
Note 7. Some American writers claim that this change from the thick cut to that of maximum brilliancy was made by an American cutter, Henry D. Morse. It was, however, as explained, necessitated by the absolute roundness of the new cut. Mr. Morse may have invented it independently in America. But it is highly probable that it originated where practically all of the world's diamonds were polished, in Amsterdam or Antwerp, where also mechanical bruting was first introduced.
Other designs for the brilliant have been tried, mostly attempts to decrease the loss of weight in cutting without impairing the brilliancy of the diamond, but they have not met with success.
We may note here that the general trend of European diamond polishing as opposed to Indian is the constant search for greater brilliancy, more life, a more vivid fire in the diamond, regardless of the loss of weight. The weight of diamond removed by bruting and by polishing amounts in even the most favourable cases to 52 per cent. of the original rough weight for a perfectly cut brilliant. In the next chapters the best proportions for a brilliant will be calculated without reference to the shape of a rough diamond, and it will be seen how startlingly near the calculated values the modern well-cut brilliant is polished.
It is to light, the play of light, its reflection and its refraction, that a gem owes its brilliancy, its fire, its colour. We have therefore to study these optical properties in order to be able to apply them to the problem we have now before us : the calculation of the shape and proportions of a perfectly cut diamond.
Of the total amount of light that falls upon a material, part is returned or reflected ; the remainder penetrates into it, and crosses it or is absorbed by it. The first part of the light produces what is termed the " lustre " of the material. The second part is completely absorbed if the material is black. If it is partly absorbed the material will appear coloured, and if transmitted unaltered it will appear colourless.
The diamonds used as gems are generally colourless or only faintly coloured ; it can be taken that all the light that passes into the stones passes out again. The lustre of the diamond is peculiar to that gem, and is called adamantine for that reason. It is not found in any other gem, although zircon and demantoid or olivine have a lustre approaching somewhat to the adamantine.
In gem stones of the same kind and of the same grade of polish, we may take it that the lustre only varies with the area of the gem stone exposed to the light, and that it is independent of the type of cut or of the proportions given to the gem (in so far as they do not affect the area) ; this is why gems where the amount of light that is reflected upon striking the surface is great, or where much of the light that penetrates into the stone is absorbed and does not pass out again, are frequently cut in such shapes as the cabochon (fig. 12), so as to get as large an area as possible, and in that way take full advantage of the lustre.
In a diamond, the amount of light reflected from the surface is much smaller than that penetrating into the stone ; moreover, a diamond is practically perfectly transparent, so that all the light that passes into the stone has to pass out again. This is why lustre may be ignored in the working out of the correct shape for a diamond, and why any variation in the amount of light reflected from the exposed surface due to a change in that surface may be considered as negligible in the calculations.
The brilliancy or, as it is sometimes termed, the " fire " or the " life " of a gem thus depends entirely upon the play of light in the gem, upon the path of rays of light in the gem. If a gem is so cut or designed that every ray of light passing into it follows the best path possible for producing pleasing effects upon the eye, then the gem is perfectly cut. The whole art of the lapidary consists in proportioning his stone and disposing his facets so as to ensure this result.
If we want to design a gem or to calculate its best shape and proportions, it is clear that we must have sufficient knowledge to be able to work out the path of any ray of light passing through it. This knowledge comprises the essential part of optics, and the laws which have to be made use of are the three fundamental ones of reflection, refraction, and dispersion.
Reflection occurs at the surface which separates two different substances or media ; a portion or the whole of the light striking that surface is thrown back, and does not cross over from one medium into another. This is the reflected light. There are different kinds of reflected light according to the nature of the surface of reflection. If that surface is highly polished, as in the case of mirrors, or polished metals or gems, the reflection is perfect and an image is formed. The surface may also be dull or matt to a greater or smaller extent (as in the case of, say, cloth, paper, or pearls). The reflected light is then more or less scattered and diffused.
It is the first kind of reflection that is of importance to us here, as diamond, owing to its extreme hardness, takes a very high grade of polish and keeps it practically for ever.
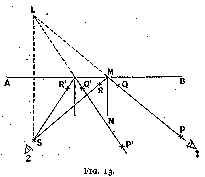
The laws of reflection can be studied very simply with a few pins and a mirror placed at right angles upon a flat sheet of paper.
A plan of the arrangement is shown in fig. 13. The experiment is as follows :--
A straight line A B is drawn upon the paper, and the mirror is stood on the paper so that the plane of total reflection (i.e. the silvered surface) is vertically over that line. Two pins P and Q are stuck anyhow on the paper, one as near the mirror and the other as far away as possible. Then the eye is placed in line with P Q at 1, so that Q is hidden by P. Without moving the eye, two more pins R and S are inserted, one near to and the other far from the mirror, in such positions that their images appear in the mirror to lie along P Q continued.
If the eye is now sighted from position 2 along S R, Q and P will appear in the mirror to lie on S R continued.
The mirror is now removed, P Q and S R are joined and will be found to intersect on A B at M. If a perpendicular M N be erected on A B at that point, the angles N M P and N M S will be found equal.
The above experiment may be repeated along other directions, but keeping the pin S at the same point. The line of sight will now lie on P' Q', and the angles between P' Q', S R' and the normal will again be found equal.
In the first experiment S appeared to lie on the continuation of P Q, in the second it appears to be situated on P' Q' produced. Its image is thus at the intersection of these two lines, at L. It can easily be proved by elementary geometry (from the equality of angles) that the image L of the pin is at the same distance from the mirror as the pin S itself, and is of the same size.
If the pins P, Q, R, S in the first experiment be placed so that their heads are all at the same height above the plane sheet of paper, and the eye be placed in a line of sight with the heads P, Q, the images of the heads R, S in the mirror will be hidden by the head of pin P.
The angle N M P (position I) is called the angle of incidence, and the angle N M S angle of reflection.
The laws of reflection (verified by the above tests) can now be formulated as follows :--
From I it follows, as shown, that
When light passes from one substance to another it suffers changes which are somewhat more complicated than in the case of reflection. Thus if we place a coin at the bottom of a tumbler which we fill with water, the coin appears to be higher than when the tumbler was empty ; also, if we plunge a pencil into the water, it will seem to be bent or broken at the surface, except in the particular case when the pencil is perfectly vertical.
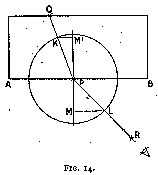
We can study the laws of refraction in a manner somewhat similar to that adopted for the reflection tests. Upon a flat sheet of paper (fig. 14) we place a fairly thick rectangular glass plate with one of its edges (which should be polished perpendicularly to the plane of the paper) along a previously drawn line A B. We place a pin, P, close to the edge A B of the glass plate and another, Q, close to the further edge. Looking through the surface A B, we place our eye in such a position that the pin Q as viewed through the glass is covered by the pin P. Near to the eye and in the same line of sight we stick a third pin R, which therefore covers pin P. The glass plate is now removed. P Q and P R are joined, a perpendicular to A B, M M', is erected at P, and a circle of any radius drawn with P as centre. This circle cuts P Q at K and R P at L. L M and K M' are drawn perpendicular to M M', L M and K M' are measured and the ratio (L M) / (K M') found.
The experiment is repeated for different positions of P and Q and the corresponding ratio (L M) / (K M') calculated. It will be found that for a given substance (as in this case glass) this ratio is constant. It is generally called the index of refraction, and generally represented by the letter n.
Referring to fig. 14, we note that as
P K = P L = radius of the circle,
we can write
L MWriting the angle of incidence R P M as i,
and the angle of refraction Q P M' as r, this equation becomes
n = (sin i) / (sin r) (Eq. 1)
or
n sin r = sin i (Eq. 2)
In this case the incident ray is in air, the index of refraction of which is very
nearly unity. With another substance it can be shown that equation (2) becomes
n sin r = n' sin i (Eq. 3)
where n' is the index of refraction of that substance.
It can be seen easily, and in a way similar to that used with reflection (i.e. sighting along the heads of pins), that in refraction also :
The paths of the incident and of the refracted ray lie in the same plane.
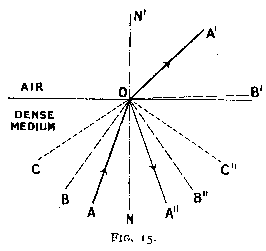
Of two substances with different index of refraction, that which has the greater index of refraction is called optically denser. In the experiment the light passed from air to glass, which is of greater optical density. Let us now consider the reverse case, i.e. when light passes from one medium to another less dense optically. Suppose a beam of light A O (fig. 15) with a small angle of incidence passes from water into air. At the surface of separation a small portion of it is reflected to A" (as we have seen under reflection). The remainder is refracted in a direction O A' which is more divergent from the normal N O N' than A O.
Suppose now that the angle A O N gradually increases. The proportion of reflected light also increases, and the angle of refraction N' O A' increases steadily and at a more rapid rate than N O A, until for a certain value of the angle of incidence B O N the refracted angle will graze the surface of separation. It is clear that under these conditions the amount of light which is refracted and passes into the air is zero. If the angle of incidence is still greater, as at C O N, there is no refracted ray, and the whole of the light is reflected into the optically denser medium, or, as it is termed, total reflection then occurs. The angle B O N is called the critical angle, and can easily be calculated by (3) when the refractive indices n and n' are known. It will be noted that when the angle of incidence attains its critical value i', the angle of refraction becomes a right angle, i.e. its sine becomes equal to unity.
Substituting in (3),
n sin r = n' sin i'Or, if the less dense medium be air,
n = 1Note 8. No mention is made here of double refraction, as the diamond is a singly refractive substance, and it was considered unnecessary to introduce irrelevant matter.
This formula (5) is very important in the design of gems, for by its means the critical angle can be accurately calculated. A precious stone, especially a colourless and transparent one like diamond, is cut to the best advantage and with the best possible effect when it sends to the spectator as strong and as dazzling a beam of light as possible. Now a gem, not being in itself a source of light, cannot shine with other than reflected light. The maximum amount of light will be given off by the gem if the whole of the light that strikes it is reflected by the back of the gem, i.e. by that part hidden by the setting, and sent out into the air by its front part. The facets of the stone must therefore be so disposed that no light that enters it is let out through its back, but that it is wholly reflected. This result is obtained by having the facets inclined in such a way that all the light that strikes them does so at an angle of incidence greater than the critical angle. This point will be further dealt with in a later chapter.
The following are a few indices of refraction which may be useful or of interest :--
Water 1.33
Crown glass 1.5 approx.
Quartz 1.54 - 1.55
Flint glass 1.576
Colourless strass 1.58
Spinel 1.72
Almandine 1.79
Lead borate 1.83
Demantoid 1.88
Lead silicate 2.12
Diamond 2.417 (Eq. 6)
[9]
These indices have, of course, been found by methods more accurate than the tests described. One of these methods, one particularly suitable for the accurate determination of the indices of refraction in gems, will be explained later.
With this value for the index of refraction of diamond, the critical angle
works out at
1
sin i = ---
n
1
= ------- = 0.4136
2.417
i = arcsin(0.4136)
i = 24° 26' (Eq. 7)
This angle will be found very important.
What we call white light is made up of a variety of different colours which produce white by their superposition. It is to the decomposition of white light into its components that are due a variety of beautiful phenomena like the rainbow or the colours of the soap bubble -- and, it may be added, the " fire " of a diamond.
The index of refraction is found to be different for light of different colours, red being generally refracted least and violet most, the order for the index of the various colours being as follows :--
Red, orange, yellow, green, blue, indigo, violet.
Note 9. In the list given above the index of refraction is that of the yellow light obtained by the incandescence of a sodium salt. This colour is used as a standard, as it is very bright, very definite, and easily produced.
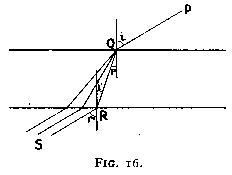
If white light strikes a glass plate with parallel surfaces
(fig. 20) the different
colours are refracted as shown when passing into the glass. Now for every colour
the angle of refraction is given by (equation (2))
n sin r = sin i
When passing out of the glass, the angle of refraction is given by
n sin i' = sin r'
As the faces of the glass are parallel, i' = r.
Therefore, r' = i, and the ray when leaving the glass is parallel to its original direction. The various colours will thus follow parallel paths as shown in fig. 16, and as they are very nearly together (the dispersion is very much exaggerated), they will strike the eye together and appear as white. This is why in the pin experiments on refraction, dispersion was not apparent to any extent.
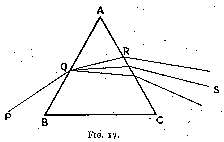
If, instead of using parallel surfaces as in a glass plate, we place them at an angle, as in a prism, light falling upon a face of the prism will be dispersed as shown in fig. 17 ; and, when leaving by another face, the light, instead of combining to form white (as in a plate), is still further dispersed and forms a ribbon of lights of the different colours, from red to violet. Such a ribbon is called a spectrum. The colours of a spectrum cannot be further decomposed by the introduction of another prism.
The difference between the index of refraction of extreme violet light and that of extreme red is called dispersion.[10] Dispersion, on the whole, increases with refractive index, although with exception. The dispersion of a number of gems and glasses is given below :--
Quartz 0.013
Sapphire 0.018
Crown glass 0.019
Spinel 0.020
Almandine 0.024
Flint glass 0.036
Diamond 0.044
Demantoid 0.057
Note 10. Generally two definite points on the spectrum are chosen ; the values given here for gems are those between the B and G lines of the solar spectrum.
Editor's note 4 has more details. -- Ed.
The greater the dispersion of a medium, other things being equal, the greater the difference between the angles of refraction of the various colours, and the further separated do they become. It is to its very high dispersion (the greatest of all colourless gem-stones) that the diamond owes its extraordinary " fire." For when a ray of light passes through a well-cut diamond, it is refracted through a large angle, and consequently the colours of the spectrum, becoming widely separated, strike a spectators eye separately, so that at one moment he sees a ray of vivid blue, at another one of flaming scarlet or one of shining green, while perhaps at the next instant a beam of purest white may be reflected in his direction. And all these colours change incessantly with the slightest motion of the diamond.
The effect of refraction in a diamond can be shown very interestingly as follows :-- A piece of white cardboard or fairly stiff paper with a hole about half an inch in diameter in its centre is placed in the direct rays of the sun or another source of light. The stone is held behind the paper and facing it in the ray of light which passes through the hole. A great number of spots of the most diverse colours appear then upon the paper, and with the slightest motion of the stone some vanish, others appear, and all change their position and their colour. If the stone is held with the hand, its slight unsteadiness will give a startling appearance of life to the image upon the paper. This life is one of the chief reasons of the diamond's attraction, and one of the main factors of its beauty.
In the study of refraction it was pointed out that the manner by which the index of refraction was calculated there, although the simplest, was both not sufficiently accurate and unsuitable for gem-stones. One of the best methods, and perhaps the one giving the most correct results, is that known as method of minimum deviation. Owing to the higher index of refraction of diamond it is especially suitable in its case, where others might not be convenient.
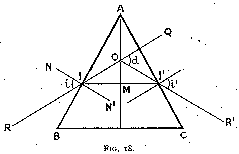
The theory of the method is as follows :--
Let A B C be the section of a prism of the substance the refraction index of which we want to calculate (fig. 18). A source of light of the desired colour is placed at R, and sends a beam R I upon the face A B of the prism. The beam R I is broken, crosses the prism in the direction I I', is again broken, and leaves it along I' R'. Supposing now that we rotate prism A B C about its edge A. The direction of I' R' changes at the same time ; we note that as we gradually turn the prism, I' R' turns in a certain direction. But if we go on turning the prism, I' R' will at a certain moment stop and then begin to turn in the reverse direction, although the rotation of the prism was not reversed. We also note that at the moment when the ray is stationary the deviation has attained its smallest value. It is not difficult to prove that this is the case when the ray of light passes through the prism symmetrically, i.e. when angles i and i' (fig. 18) are equal.
Let A M be a line bisecting the angle A. Then I I' is perpendicular to A M. Let R I be produced to Q and R' I' to O. They meet on A M and the angle Q O R' is the deviation d (i.e. the angle between the original and the final direction of the light passing through the prism).
Therefore O I I' = ½ d.
Draw the normal at I, N N'.
Then
M I N' = I A M = ½ a
if a be the angle B A C of the prism.
Now by equation (1)
n = (sin i) / (sin r)
i = N I R = O I N' = O I M + M I N'
= ½ d + ½ a = ½ (d+a)
r = M I N' = ½ a
therefore
n = (sin ½(d+a)) / (sin ½a)
(Eq. 8)
The index of refraction can thus be calculated if the angles d and a are known. These are found by means of a spectroscope. This instrument consists of three parts : the collimator, the table, and the telescope. The light enters by the collimator (a long brass tube fitted with a slit and a lens) passes through the prism which is placed on the table, and leaves by the telescope. The collimator is usually mounted rigidly upon the stand of the instrument. Its function is to determine the direction of entry of the light and to ensure its being parallel. Both the table and the telescope are movable about the centre of the table, and are fitted with circular scales which are graduated in degrees and parts of a degree, and by means of which the angles are found.
Now two facets of a stone are selected, and the stone is place upon the table so that these facets are perpendicular to the table. The angle a of the prism, i.e. the angle between these two facets, can be found by direct measurement with a goniometer or also by the spectroscope. The angle d is found as follows :-- The position of the stone is arranged so that the light after passing through the collimator enters it from one selected facet and leaves it by the other. The telescope is moved until the spectral image of the source of light is found. The table and the stone are now rotated in the direction of minimum deviation, and at the same time the telescope is moved so that the image is kept in view. We know that at the point of minimum deviation the direction of motion of the telescope changes. When this exact point is reached the movements of the stone and of the telescope are stopped, and the reading of the angle of deviation d is taken on the graduated scale.
The values of a and d are now introduced in equation (8) :
n = (sin ½(d+a)) / (sin ½a)
(Eq. 8)
and the value of n calculated with the help of sine tables or logarithms.
The values for diamond are
n = 2.417 for sodium light
Dispersion = nred - nviolet
= 0.044
In the survey of the history of diamond cutting, perhaps the most remarkable fact is that so old an art should have progressed entirely by trial and error, by gradual correction and slow progress, by the almost accidental elimination of faults and introduction of ameliorations. We have traced the history of the art as far back as 1375, when the earliest recorded diamond manufacturers existed, and when the polishers had already attained a high degree of guild organisation. We have every reason to believe that the process of diamond polishing was known centuries before. And yet all these centuries, when numerous keen minds were directed upon the fashioning of the gem, have left no single record of any purposeful planning of the design of the diamond based upon fundamental optics. Even the most bulky and thorough contemporary works upon the diamond or upon gems generally rest content with explaining the basic optical principles, and do no more than roughly indicate how these principles and the exceptional optical properties of the gem explain its extraordinary brilliancy ; nowhere has the author seen calculations determining its best shape and proportions. It is the purpose of the present chapter to establish this shape and these proportions. The diamond will be treated essentially as if it were a worthless crystal in which the desired results are to be obtained, i.e. without regard to the great value which the relation between a great demand and a very small supply gives to the least weight of the material.
It is useful to recall here the principles and the properties which will be used in the calculations.
Reflection
Refraction
If the first medium is air, n' = 1, and equation becomes
n sin r = (sin i) (Eq. 2)
When a ray of light passes from one medium into another optically less dense,
total reflection occurs for all values of the angle of incidence above a certain
critical value. This critical angle is give by equation
n
sin i' = --- (Eq. 4)
n'
Or, if the less dense medium be air,
1
sin i' = --- (Eq. 5)
n'
Dispersion
When a ray of light is refracted, dispersion occurs, i.e. the ray is split up into a band or spectrum of various colours, owing to the fact that each colour has a different index of refraction. The dispersion is the difference between these indices for extreme rays on the spectrum.
Data
In a diamond :
Index of refraction : n = 2.417 (for a sodium light)
dispersion : delta = 0.044
critical angle : i' = 24° 26' (Eq. 7)
Postulate. -- The design of a diamond or of any gem-stone must be symmetrical about an axis, for symmetry and regularity in the disposition of the facets are essential for a pleasing result.
Let us now consider a block of diamond bounded by polished surfaces, and let us consider the effect on the path of light of a gradual change in shape ; we will also observe the postulate and keep the block symmetrical about its axis.
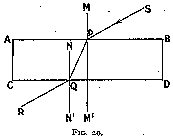
Let us take as first section one having parallel faces (fig. 20), and let M M' be its axis of symmetry. Let us for convenience place the axis of symmetry vertically in all future work, so that all surfaces crossing it are horizontal.
Consider a ray of light S P striking face A B. It will be refracted along P Q and
leave by Q R, parallel to S P (as we have seen in studying dispersion). We also know
that if N N' is the normal at Q, angles N Q P and Q P M' are equal. Therefore, for
total reflection
Q P M' == 24° 26'
but at that angle of refraction the angle of incidence S P M becomes a right angle and no light penetrates the stone. It is thus obvious that parallel faces in a gem are very unsatisfactory, as all the light passing in by the front of a gem passes out again by the back without any reflection.
We can avoid parallelism by inclining either the top or bottom faces at an angle with the direction A B. In the first case, we obtain the shape of a rose-cut diamond and in the second case that of a brilliant cut. We will examine the rose cut in the first instance.
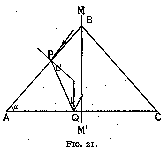
Consider (fig. 21) a section having the bottom surfaces horizontal, and let us incline the top surface A B at an angle alpha with it. To maintain symmetry, another surface B C is introduced. We have now to find the value of alpha for which total reflection occurs at A C. Now for this to be the case, the minimum angle of incidence upon A C must be 24° 26'. Let us draw such an incident ray P Q. To ensure that no light is incident at a smaller angle, we must make the angle of refraction at entry 24° 26' and arrange the surface of entry as shown, A B, for we know that then no light will enter at an angle more oblique to A B or more vertical to A C. This gives us a value of twice the critical angle, i.e. 48° 52'. Such a section is very satisfactory indeed as regards reflection, as, owing to its derivation, all the light entering it leaves by the front part. Is it also satisfactory as regards refraction ?
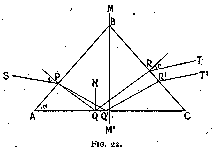
Let us follow the path of a ray of light of any single colour of the spectrum, S P Q R T (fig. 22). Let i and r be the angles of incidence upon and of refraction out of the diamond.
At Q, P Q N = R Q N, and therefore in triangles A P Q and R C Q
angle A Q P = angle C Q R
Also by symmetry A = C,
therefore
angle A P Q = angle C R Q
it follows that i = r.
As the angle i is the same for all colours of a white ray of light, the various colours will emerge parallel out of the diamond and give white light. This is the fundamental reason of the unpopularity of the rose ; there is no fire.
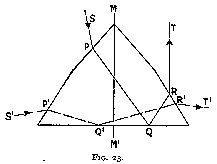
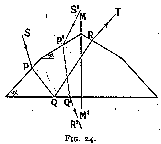
This effect may be remedied to a small extent by breaking the inclined facet (figs 23 and 24), so that the angle be not the same at entry as at exit. This breaking is harmful to the amount of light reflected whichever way we arrange it ; if we steepen the facet near the edge, there is a large proportion of light projected backwards and being lost, for we may take it that the spectator will not look at the rose from the side of the mounting (fig. 23). If, on the other hand, we flatten the apex of the rose (fig. 24) (which is the usual method), a leakage will occur through its base. There is, of course, no amelioration in the refraction if the light passes from one facet to another similarly placed (as shown in fig. 23, path S' P' Q' R' T'). Taking the effect as a whole, the least unsatisfactory shape is as shown in fig. 24, with the angles alpha about 49° and 30° for the base and the apex respectively. The rose cut, however, is fundamentally wrong, as we have seen above, and should be abolished altogether. It is the high cost of the material that is the cause of its still being used in cases where the rough shape is especially suitable, and then only in small sizes. In actual practice the proportions of the cut rose depend largely upon those of the rough diamond, the stone being cut with as small a loss of material as possible. Generally the values of alpha are much below those given above, i.e. 49° and 30°, as where the material is thick enough to allow such steep angles it is much better to cut it into a brilliant.
A. Back of the Brilliant
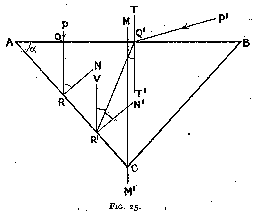
Let us now pass to the consideration of the other alternative, i.e. where the top surface is a horizontal plane A B and where the bottom surface A C is inclined at an angle alpha to the horizontal (fig. 25). As before, we have to introduce a third plane B C to have a symmetrical section.
First Reflection
Let a vertical ray P Q strike A B. As the angle of incidence is zero,
it passes into the stone without refraction and meets plane A C at R. Let R N be
the normal at that point, then, for total reflection to occur,
angle N R Q = 24° 26'
But
angle N R Q = angle Q A R = alpha
as A Q and Q R, A R and R N are perpendicular.
Therefore, for total reflection of a vertical ray,
alpha = 24° 26'
Let us now incline the ray P Q so that it gradually changes from a vertical
to a horizontal direction, and let P' Q' be such a ray. Upon passing into the diamond
it is refracted, and strikes A C at an angle Q' R' N' where R' N' is the normal to A C.
When P' Q' becomes horizontal, the angle of refraction T' Q' R' becomes equal
to 24° 26'. This is the extreme value attainable by that angle ;
also, for total reflection, angle Q' R' N' must not be less than 24° 26'.
If we draw R' V, vertical angle V R' Q = R' Q' T' = 24° 26', and
angle V R' N' = V R' Q' + Q' R' N'
= 24° 26' + 24° 26'
= 48° 52'
as before,
alpha = angle V R' N'
and therefore
alpha = 48° 52' (Eq. 9)
For absolute total reflection to occur at the first facet, the inclined facets must make an angle of not less than 48° 52' with the horizontal.
Second Reflection
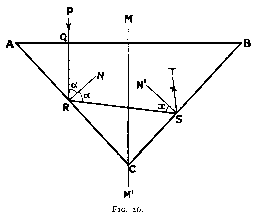
When the ray of light is reflected from the first inclined facet A C (fig. 26),
it strikes the opposite one BC. Here too the light must be totally reflected,
for otherwise there would be a leakage of light through the back of the gem-stone.
Let us consider, in the first instance, a ray of light vertically incident upon the stone.
The path of the ray will be P Q R S T. If R N and S N' are the normals at R and S
respectively, then for total reflection,
angle N' S R = 24° 26'
Let us find the value of alpha to fulfil that condition :
angle Q R N = angle Q A R = alpha
as having perpendicular sides.
angle S R N = angle Q R N
as angles of incidence and reflection.
Therefore
angle N R S = alpha
Now let
angle N' S R = x
Then, in triangle R S C,
angle S R C = 90° - alpha
angle R S C = 90° - x
angle R C S = 2 * angle R C M
= 2 * angle A R Q
= 2 * (90° - alpha)
The sum of these three angles equals two right angles,
90° - alpha + 90° - x
+ 180° - 2 alpha = 180°
or
3 alpha + x = 180°
3 alpha = 180° - x
Now, x is not less than 24° 26',
therefore alpha is not greater than
180° - 24° 26'
alpha = ---------------- = 51° 51'
3
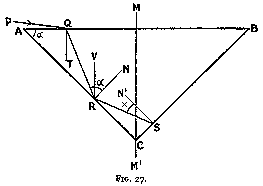
Let us again incline P Q from the vertical until it becomes horizontal, but in this case in the other direction, to obtain the inferior limit.
Then (fig. 27) the path will be P Q R S. Let Q T , R N, S N' be the normals at Q, R, and S respectively. At the extreme case, T Q R will be 24° 26'. Draw R V vertical at R.
Then
angle Q R V = angle T Q R = 24° 26'
angle V R N = alpha
As before, in triangle R S C,
angle S R C = 90° - angle N R S
= 90° - alpha - 24° 26'
angle R C S = 2 * (90° - alpha)
angle R S C = 90° - x
Then
90° - alpha - 24° 26' + 180° - 2 alpha
+ 90° - x = 180°
3 * alpha + x = 180° - 24° 26' = 155° 34'
In the case now considered,
x = 24° 26'
Then
3 * alpha = 155° 34' - x = 131° 8'
alpha = 43° 43' (Eq. 10)
For absolute total reflection at the second facet, the inclined facets must make an angle of not more than 43° 43' with the horizontal.
We will note here that this condition and the one arrived at on page 66 [Eq. 9 -- Ed.] are in opposition. We will discuss this later, and will pass on now to considerations of refraction.
Refraction
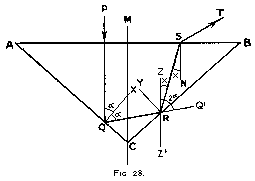
First case : alpha is less than 45°
In the discussion of refraction in a diamond, we have to consider two cases, i.e. alpha is less than 45° or it is more than 45°. Let us take the former case first and let P Q R S T (fig. 28) be the path of the ray. Then, if S N is the normal at S, we know that for total reflection at S angle R S N = 24° 26'. We want to avoid total reflection, for if the light is to be thrown back into the stone, some of it may be lost, and in any case the ray will be broken too frequently and the result will be disagreeable.
Therefore,
angle R S N < 24° 26' (Eq. 11)
Suppose this condition is fulfilled and the light leaves the stone along S T. It is refracted, and its colours are dispersed into a spectrum. It is desirable to have this spectrum as long as possible, so as to disperse the various colours far away from each other. As we know, this will give us the best possible " fire ".
This result will be obtained when the ray is refracted through the maximum angle.
By (11) the value for that angle is 24° 26', and (11) becomes
angle R S N = 24° 26' for maximum dispersion.
But then the light leaves A B tangentially, and the amount of light passing is zero.
To increase that amount, the angle of refraction has to be reduced : the angle of
dispersion decreases simultaneously, but the amount of light dispersed increases
much more rapidly.
Now we know that the angle of dispersion is proportional to the sine
of the angle of refraction. It is, moreover, proved in optics that the amount
of light passing through a surface as at A B is proportional to the cosine
of the angle of refraction. The brilliancy produced is proportional both to the amount
of light and to the angle of dispersion, and therefore to their product, and
(by the theory of maxima and minima) will be maximum when they are equal,
i.e. when the sine and cosine of the angle of refraction are equal.
For maximum brilliancy, therefore, the angle of refraction should be 45°.
This gives for angle R S N
sin 45° 0.7071
sin R S N = --------- = -------- = 0.2930
2.417 2.417
therefore
angle R S N = 17° for optimum brilliancy (Eq. 12)
Let (fig. 28) Q X and R Y be the normals at Q and R respectively, and let Z Z' be vertical through R.
We know that
angle R Q X = angle P Q X = alpha
therefore
angle P Q R = 2 * alpha
Produce Q R to Q'.
Then, as P Q and Z Z' are parallel,
angle Z R Q' = angle P Q R = 2 * alpha
Now, let
angle R S N = x ( = 17° for optimum brilliancy)
Then, as Z Z' and S N are parallel,
angle Z R S = x
As they are complements to angles of incidence,
angle Q R C = angle S R B = i (say)
but
angle Q' R B = angle Q R C
therefore
angle S R Q' = 2i
In angle Z R Q' we have
angle Z R Q' = angle Z R S + angle S R Q'
2 * alpha = x + 2 * i (Eq. 13)
In triangle Q C R
angle R Q C = 90° - alpha
angle Q R C = i
angle Q C R = 2 * (90° - alpha)
therefore
(90° - alpha) + i + 180° - 2 * alpha
= 180°
or
i = 3 * alpha - 90°
Introduce this value of i in (13),
2 * alpha = x + 6 * alpha - 180°
4 * alpha = 180° - x
and giving x its value 17°,
4 * alpha = 180° - 17° = 163°
alpha = 40° 45' (Eq. 14)
If we adopt this value for alpha, the paths of oblique rays will be as shown in fig. 29, P Q R S T when incident from the left of the figure, and P' Q' R' S' T' when incident from the right. Ray P Q R S T will leave the diamond after the second reflection, but with a smaller refraction than that of a vertically incident ray, and therefore with less " fire." Oblique rays incident from the left are, however, small in number owing to the acute angle Q R A with which they strike A C ; the loss of fire may therefore be neglected.
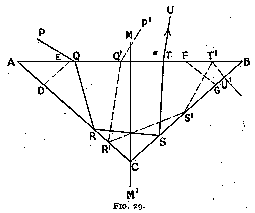
Ray P' Q' R' S' T' will strike A B at a greater angle of incidence than 24° 26', and will be reflected back into the stone. This is a fault that can be corrected by the introduction of inclined facets D E, F G ; ray P' Q' R' S' T' will then strike F G at an angle less than 24° 26', and this angle can be arranged by suitably inclining F G to the horizontal so as to give the best possible refraction. The amelioration obtained by thus taking full advantage of the refraction is so great that the small loss of light caused by that arrangement of facets is insignificant : the leakage occurs through the facet C B, near C, where the introduction of the facet D E allows light to reach C B at an angle less than critical. In a brilliant, where C B is the section of the triangular side of an eight sided pyramid, the area near the apex C is very small, and the leakage may therefore be considered negligible.
Second case : alpha is greater than 45°
In this case the path of a vertical ray will be shown by P Q R S T in fig. 30,
and the optimum value for alpha, which may be calculated as before,
will be
alpha = 49° 13' (Eq. 15)
As regards the vertical rays, this value gives a fire just as satisfactory as (14) (alpha = 40° 45'); let us consider what happens to oblique rays.
Rays incident from the left as p q r s t u may strike B C at an angle of incidence less than the critical, and will then leak out backwards. Or they may be reflected along s t, and may then be reflected into the stone. Both alternatives are undesirable, but they do not greatly affect the brilliancy of the gem, because, as we have seen, the amount of light incident from the left is small.
That incident from the right is, on the contrary, large.
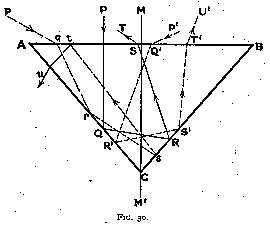
Let us follow ray P' Q' R' S' T'. It will be reflected twice, and will leave the diamond after the second reflection, like the vertically incident ray, but with a smaller refraction, and consequently less fire ; most of the light will be striking the face A B nearly vertically when leaving the stone, and the fire will be very small. This time it is impossible to correct the defect by introducing accessory facets, as the paths S' T' of the various oblique rays are not localised near the edge B, but are spread over the whole of the face ; we are therefore forced to abandon this design.
Summary of the Results obtained for alpha
We have found that--
Upon consideration of the above results, we conclude that the correct value
for alpha is 40° 45', and gives the most vivid fire and the greatest
brilliancy, and that although a greater angle would give better reflection,
this would not compensate for the loss due to the corresponding reduction
in dispersion. In all future work upon the modern brilliant
we will therefore take
alpha = 40° 45'
The editor's notes show that Tolkowsky's analysis is still valid even for diamonds that have a different pavilion angle. Tolkowsky provides a way to calculate how the best crown angle and table size depend on each diamond's actual pavilion angle. -- Ed.
B. Front of the Brilliant
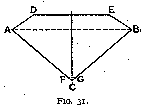
When arriving at the value of alpha = 40° 45', we have explained how the use of that angle introduced defects which could be corrected by the use of extra facets. The section will therefore be shaped somewhat as in fig. 31. It will be convenient to give to the different facets the names by which they are known in the diamond-cutting industry. These are as follows :--
A C and B C are called pavilions or quoins
(according to their position relative to the axis of crystallisation of the diamond).A D and E B are similarly called bezels or quoins.
D E is the table.
F G is the culet,
which is made very small and whose only purpose is to avoid a sharp point.
Through A and B passes the girdle of the stone.
We have to find the proportions and inclination of the bezels and the table. These are best found graphically. We know that the introduction of the bezels is due to the oblique rays ; it is therefore necessary to study the distribution of these rays about the table, and to find what proportion of them is incident in any particular direction.
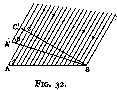
Consider a surface A B (fig. 32) upon which a beam of light falls at an angle alpha. Let us rotate the beam so that the angle becomes beta (for convenience, the figure shows the surface A B rotated instead of A' B, but the effect is the same). The light falling upon A B can be stopped in the first case by intercepting it with screen B C, and in the second with a screen B C' where B C C' is at right angles to the direction of the beam. And if the intensity of the light is uniform, the length of B C and B C' will be a measure of the amount of light falling upon A B and A B' respectively.
Now
B C = A B sin alpha
B C' = A'B sin beta = A B sin beta
Therefore, other things being equal, the amount of light falling upon a surface is proportional to the sine of the angle between the surface and the direction of the light. We can put it as follows :--
If uniformly distributed light is falling from various directions upon a surface A B, the amount of light striking it from any particular direction will be proportional to the sine of the angle between the surface and that direction.
If we draw a curve between the amount of light striking a surface from any particular direction, and the angle between the surface and that direction, the curve will be a sine curve (fig. 33) if the light is equally distributed and of equal intensity in all directions.
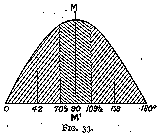
For calculations we can assume this to be the case, and we will take the distribution of the quantity of light at different angles to follow a sine law.
It is convenient to divide all the light entering the diamond into three groups, one of vertical rays and two of oblique rays, such that the amount of light entering from each group is the same. Now in the sine curve (fig. 33) the horizontal distances are proportional to the angles between the table of a diamond and the direction of the entering rays ; the vertical distances are proportional to the amount of light entering at these angles. The total amount of light entering will be proportional to the area shaded. That area must therefore be divided into three equal parts ; this may be done by integrals, or by drawing the curve on squared paper, counting the squares, and drawing two vertical lines on the paper so that one-third of the number of the squares is on either side of each line.
By integrals,
/
area = | sin x dx = - cos x
/
[ ] 180°
The total area = [ - cos x] = 1 + 1 = 2
[ ] 0°
therefore
(1/3) area = 2/3
The value of alpha corresponding to the vertical dividing lines
on the curve is thus given by
cos x = 1 - (2/3) = 1/3
cos x = 1 - (4/3) = - 1/3
therefore
x = 70½°
approximately
and
x = 109½°
Taking the value x = 90° as zero for reckoning the angles of incidence,
i = 90° - 70½° = 19½°
and
i = 90° - 109½° = -19½°
The corresponding angles of refraction are
sin i sin 19½° 0.3333
sin r = ------- = ---------- = -------- = 0.1377
n 2.417 2.417
r = 7° 52'
The range of the different classes is thus as follows :--
Angle of incidence:
vertical rays -19½° to +19½°
oblique rays -90° to +19½°
and +19½° to +90°
Angle of refraction:
vertical rays -7° 52' to +7° 52'
oblique rays -24° 26' to +7° 52'
and +7° 52' to +24° 26'
The average angle of each of these classes may be obtained by dividing each of the
corresponding parts on the sine curve into two equal parts. The results are
as follows :--
Angle of incidence:
vertical rays 0°
oblique rays -42°
and +42°
Angle of refraction:
vertical rays 0°
oblique rays -16°
and +16°
For the design of the tables and bezels, we have to know the directions and positions of the rays leaving the stone. The values just obtained would enable us to do so if all the rays entering the front of the gem also left there. We have, however, adopted a value for alpha (alpha = 40° 45') which we know permits leakage, and we have to take that leakage into consideration.
The angle where leakage begins is inclined at 24° 26' to the pavilion
(fig. 25).
We have thus
Q' R' N' = 24° 26'
therefore
Q' R' A = 90° - 24° 26' = 65° 34'
Now in triangle A Q' R',
Q' R' A + A Q' R' + R' A Q' = 180°
therefore
A Q' R' = 180° - 65° 34' - 40° 45'
= 73° 41'
The limiting angle of refraction R' Q' T is thus
= 90° - 73° 41' = 16° 19'
corresponding to an angle of incidence of
sin i = n sin r = 2.417 sin 16° 19'
= 2.417 * 0.281 = 0.678
i = 42½°
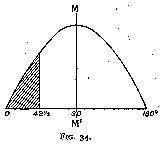
Editor's note 9 shows Tolkowsky made a rounding error. The correct angle is 42¾°. Also, fig. 34 is wrong. The 42½° is an angle of incidence, so it is measured from the vertical. In fig. 34, 0° and 180° are horizontal, and 90° (line M M') is the vertical. Using the coordinates of fig. 34, the shading should be between 0° and 47¼°. -- Ed.
Upon referring to the sine curve, we find that the area shaded (fig. 34), which represents the amount of light lost by leakage, although not so large as if the same number of degrees leakage had occurred at the middle part of the curve, is still very appreciable, forming as it does about one-sixth of the total area. Just under one-half (exactly 0.493) of the light incident obliquely from the right (fig. 25) is effective, the other half being lost by leakage. Still, the sacrifice is worth while, as it produces the best possible fire.
Editor's note 12 shows that the fraction depends on alpha. For alpha = 40° 45', the fraction = 0.518. Tolkowsky rounds it off to 0.493. -- Ed.
The oblique rays incident from the right range therefore 19½° to 42½°, with an average (obtained as before) of 30° 15'. The corresponding refracted rays are 7° 52', 16° 19', and 12° 0'.
We have now all the information necessary for the design of the table and the bezels.
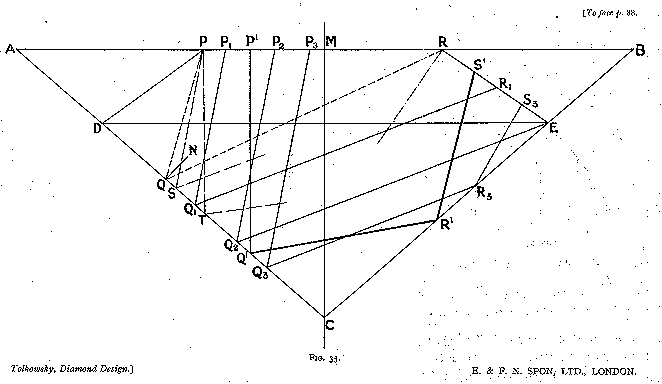
Design of Table and Bezels (fig. 35)
Let us start with the fundamental section A B C symmetrical about M M', making the angles C A B and A B C 40° 45'.
The bezels have been introduced into the design to disperse the rays which were originally incident from the right upon facet A B. To find the limits of the table, we have therefore to consider the path of the limiting oblique ray. We know that this ray has an angle of incidence of 42½° and an angle of refraction of 16° 19'. Let us draw such a ray P Q: it will be totally reflected along Q R, if we make P Q N = N Q R, where Q N is the normal. Now Q R should meet a bezel.
If the ray P Q R was drawn such that M P = M R, then P and R will be the points at which the bezels should meet the table. For if P Q be drawn nearer to the centre of the stone, Q R will then meet the bezel, and if P Q be drawn further away, it will meet the opposite bezel upon its entry into the stone and will be deflected.
The first point to strike us is that no oblique rays incident from the left upon the table strike the pavilion A C, owing to the fact that the table stops at P. We will, therefore, treat them as non-existent, and confine our attention to the vertical rays and those incident from the right.
Let us draw the limiting average rays of these two groups, i.e. the rays of the average refractions 0° and 12° passing through P, P S, and P T. The length of the pavilion upon which the rays of these two groups fall are thus respectively C S and C T.
The rays of the first group P' Q' R' S' are all reflected twice before passing out of the stone, and make, after the second reflection, an angle of 17° with the vertical (as by eq. (12)). Of the rays of the second group, most are reflected once only (P1 Q1 R1) and make then an angle of 69½° with the vertical. (This angle may be found by measurement or by calculation). Part of the second group is reflected twice (P3 Q3 R3 S3), and strikes the bezel at 29° to the vertical. This last part will be considered later, and may be neglected for the moment.
We have to determine the relation between the amount of light of the first group
and the of the first part of the second group. Now we know that the amount
of oblique light reflected on pavilion A C is 0.493 of the amount of vertical light
reflected (cp. fig. 34 and context).
If we take as limit for the once-reflected
oblique ray the point E (as a trial) on pavilion B C,
i.e. if it is at E that the girdle is situated, then the corresponding
point of reflection for that oblique ray will be Q2
(fig. 35). The surface of pavilion
upon which the oblique rays then act will be limited by S and Q2, and as in a brilliant
the face A C is triangular, the surface will be proportional to
(SC * SC) - (Q2C * Q2C)
Similarly, the surface upon which the vertical group falls will be proportional to
TC * TC
Thus we have as relative amounts of light--
for vertical rays (TC * TC)
for oblique rays 0.493 * ((SC * SC) - (Q2C * Q2C))
The first group strikes the bezel at 17° to the vertical, and the second
at 69½° to the vertical. The average inclination to the vertical will
thus be
17° * (TC * TC) + 69½° * 0.493 * ((SC * SC) - (Q2C * Q2C))
------------------------------------------------------------
(TC * TC) + 0.493 * ((SC * SC) - (Q2C * Q2C))
Let us draw a line in that direction (through R, say), and let us draw a perpendicular to it through R, R E ; then that perpendicular will be the best direction for the bezel, as a facet in that direction takes the best possible advantage of both groups of rays.
If the point E originally selected was not correct, then the perpendicular through R will not pass through E, and the position of E has to be corrected and the corresponding value of C Q2 correspondingly altered until the correct position E is obtained.
For that position E (shown on fig. 35),
measures scaled off the drawing give
CS = 2.67 CS * CS = 7.12
CT = 2.13 CT * CT = 4.54 (CS * CS) - (CQ2 * CQ2) = 4.57
CQ2 = 1.60 CQ2 * CQ2 = 2.56
Therefore the average resultant inclination will be
17° * (CT * CT) + 69½° * 0.493 * ((CS * CS) - (CQ2 * CQ2))
----------------------------------------------------------
(CT * CT) + 0.493 * ((CS * CS) - (CQ2 * CQ2))
17° * 4.54 + 69½° * 0.493 * 4.57
----------------------------------
4.54 + 0.493 * 4.57
77.2° + 156.2° 233.4°
---------------- = -------- = 34.45° = 34½°
4.54 + 2.24 6.78
to the vertical.
By the construction, the angle beta, i.e. the angle between
the bezel and the horizontal, has the same value
beta = 34½°
The small proportion of oblique rays which is reflected twice meet the bezel near its edge, striking it nearly normally : they make an angle of 29° with the vertical. Facets more steeply inclined to the horizontal than the bezel should therefore be provided there. The best angle for refraction would be 29° + 17° = 46°, but if such an angle were adopted most of the light would leave in a backward direction, which is not desirable. It is therefore advisable to adopt a somewhat smaller value ; an angle of about 42° is best.
Editor's note: The inclination of the upper girdle facets must be less than 42° to the horizontal, to have a 4-sided kite facet and follow Tolkowsky's other recommendations. An upper girdle facet angle of 39° is possible. FOLDS.NET has software that lets you calculate the upper girdle facet angle. -- Ed.
The faceting which is added to the brilliant is shown in fig. 37. Near the table, " star " facets are introduced, and near the girdle, " cross " or " half " facets are used both at the front and at the back of the stone.
We have seen that it is desirable to introduce near the girdle facets somewhat steeper than the bezel, at an angle of about 42°, by which facets the twice-reflected oblique rays might be suitably refracted. The front " half " facets fulfill this purpose.
We have remarked that the angle (42°) had to be made smaller than the best angle for refraction (46°) to avoid being sent in a backward direction, where it is unlikely to meet either a spectator or a source of light.
Editor's note: Actually, the angle is even smaller (39°) so that the kite facet can have 4 sides. -- Ed.
To obviate this disadvantage, a facet two degrees steeper than the pavilion
should be introduced near the girdle on the back side of the stone ;
for then the second reflection of the oblique rays will send them
at an angle of 25° to the vertical (instead of 29°), and the best value
for refraction for the front half facets will be between
25° + 17° = 42°
These values are satisfactory also as regards the distribution of light ; for now the greater part of the light is sent not in a backward, but in a forward, direction.
The facet two or three degrees steeper than the pavilion is obtained in the brilliant by the introduction of the back " half " facet, which is, as a matter of fact, generally found to be about 2° steeper than the pavilion in well-cut stones. Where the cut is somewhat less fine and the girdle is left somewhat thick (to save weight), that facet is sometimes made 3° steeper, or even more, than the pavilion.
The " star " facet was probably introduced to complete the design of the brilliant, which without its use would be lacking in harmony, but which its introduction makes exceedingly pleasing from the point of view of the balance of lines.
Let us examine the optical consequences of the use of " star " facets.
On the one hand, their inclination -- about 15° to the horizontal -- permits a certain amount of light to leave the stone without having been sufficiently refracted. On the other, they diminish the area of the bezels and consequently decrease the leakage of light which occurs through the bezel and the opposite pavilion (owing to the surfaces being nearly parallel). They also cause a somewhat better distribution of light, for they deflect part of the rays which would otherwise have increased the strength of the spectra refracted by the bezels, and create therewith spectra along other directions ; it is true that, as seen above, these spectra will be shorter. But they will be more numerous ; and though the " fire " -- as consequent from the great dispersion of the rays of light -- will be slightly diminished, the " life " -- if we may term " life " the frequency with which a single source of light will be reflected and refracted to a single spectator upon a rotation of the stone -- will be increased to a greater degree. And if we take into account the decrease in the leakage of light, we may conclude that the introduction of the stars, on the whole, is decidedly advantageous to the brilliant.
Editor's note: The inclination of the star facets must be greater than 15° to the horizontal, to have a 4-sided kite facet and follow Tolkowsky's other recommendations. A star facet angle of 19° or 20° is possible. FOLDS.NET has software that lets you calculate the star facet angle. -- Ed.
We have thus as best section of a brilliant one as given in fig. 35, A B C D E, where
alpha = 40° 45'D E is obtained from P R in fig. 35.
Editor's notes:
Tolkowsky has just renamed the points.
The new points A D M E B C are the same as fig. 35's D P M R E C.
The new A B is the diameter in the girdle plane.
The new A B is obtained from D E in fig. 35.
The new D E is the corner-to-corner diameter of the table.
The new D E is obtained from P R in fig. 35.
M C is the gem axis, as shown in fig. 35.
M' is the intersection of the gem axis and the girdle plane. -- Ed.
If we make the diameter A B of the stone 100 units, then the main dimensions are in the following proportions (fig. 35) :--
Diameter A B 100 %Editor's note:
Tolkowsky omits the girdle and the culet.
My article on girdles shows that the girdle adds 1.7% plus the nominal girdle thickness to the overall depth. On the other hand, part of this extra thickness is offset by a smaller optimum crown angle and a larger optimum table ratio. -- Ed.
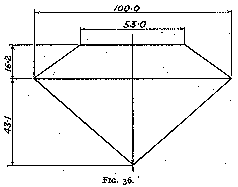
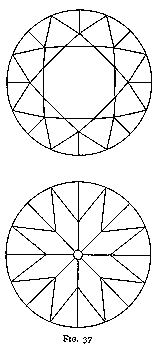
Fig. 36 shows the outline of a brilliant with these proportions.
These proportions can be approximated as follows :--
In a well-cut brilliant the diameter of the table is one-half of the total diameter, and the thickness is six-tenths of the total diameter, rather more than one-quarter of the thickness being above the girdle, and rather less than three-quarters below.
It is to be noted here that a different proportion is generally stated for the thickness above the girdle (" one-third of the total thickness "), both in works upon diamonds, and by diamond polishers themselves. It is true that diamonds were cut thicker above the girdle and with a smaller table before the introduction of sawing, for then the table was obtained by grinding away a corner or an edge of the stone, and the loss of weight was thus considerable, and would have been very much greater still if the calculated proportions had been adopted. With the use of the saw, the loss in weight was enormously reduced and the manufacture of sawn stones become therefore much finer and more in accordance with the results given above. It is a remarkable illustration of conservatism that although diamonds have been cut for decades with ¼ (approximately) of the thickness above the girdle, yet even now the rule is generally stated as 1/3 of the thickness.
Stones are still cut according to that rule, but then they are not sawn stones as a rule, and the thickness left greater to diminish the loss of weight. The brilliancy is not greatly diminished by making the stone slightly thicker over the girdle.
In the course of his connection with the diamond-cutting industry the author has controlled and assisted in the control of the manufacture of some million pounds' worth of diamonds, which were all cut regardless of the loss of weight, the only aim being to obtain the liveliest fire and the greatest brilliancy. The most brilliant larger stones were measured and their measures noted. It is interesting to note how remarkably close these measures, which are based upon empirical amelioration and rule-of-thumb correction, come to the calculated values.
As an instance the following measures, chosen at random, are given (the dimensions are in millimetres) :--
Table IThese measures, worked out in percentage terms of A B, give :--
Table IIEditor's note 37 shows that the best crown angle and table ratio depend on the actual pavilion angle. The column headings, "=", "vs.", and "~" notes, and "1% Girdle Theory" column are new in this edition. The order of the last two rows has been changed for easier reading.
The "1% Girdle Theory" column is based on my article,
"Diamond Girdles -- How Adding a Girdle Changes Marcel Tolkowsky's Diamond Design". I do not know if Tolkowsky's sample diamonds had girdles, let alone how thick they may have been. I do not know what the best girdle thickness is. It might be 1% for some diamonds; it might a larger percentage for smaller diamonds. (I measure the "girdle" by averaging the thin parts of the girdle.)Editor's note 29 shows that the "culet height" is about one-half the "culet" (diameter) reported by Sarin machines. -- Ed.
In the seventh column, the averages of the measures are worked out, and the eighth gives the calculated theoretical values. It will be noted that the values of alpha, beta, and M M' correspond very closely indeed, but that M C and M' C are very slightly less than they should be theoretically.
The very slight difference between the theoretical and the measured values is due to the introduction of a tiny facet, the collet, at the apex of the pavilions. This facet is introduced to avoid a sharp point which might cause a split or a breakage of the diamond.
What makes the agreement of these results even more remarkable is that in the manufacture of the diamond the polishers do not measure the angles, etc., by any instrument, but judge of their values entirely by eye. And such is the skill they develop, that if the angles of two pavilions of a brilliant be measured, the difference between them will be inappreciable.
We may thus say that in the present-day well-cut brilliant, perfection is practically reached : the high-class brilliant is cut as near the theoretic values as is possible in practice, and gives a magnificent brilliancy to the diamond.
That some new shape will be evolved which will cause even greater fire and life than the brilliant is, of course, always possible, but it appears very doubtful, and it seems that the brilliant will be supreme for, at any rate, a long time yet.
Ed. Note 1:
Tolkowsky shows a graphical way to determine the best crown angle and table angle
for a given pavilion angle. He tabulates the proportions
that best match just one pavilion angle (40° 45').
We can find formulas for the crown angle and table size,
so that a computer can calculate how changing the pavilion angle
changes the best crown angle and table size.
We will use the same pictures and analysis that Tolkowsky does.
Ed. Note 2:
On page 83 (near fig. 33),
Tolkowsky divides "all the light entering the diamond into three groups,
one of vertical rays and two of oblique rays, such that the light entering from
each group is the same." Using integrals, he shows that the angle of incidence
that divides the vertical rays from the oblique rays is:
i = 90° - arccos(1/3)
= 90° - 70° 31' 44"
= 19° 28' 16"
(Tolkowsky rounds this off to 19½°.)
Ed. Note 3:
The corresponding angle of refraction is
r = arcsin(sin i / n)
= arcsin( 1/3 / 2.417 )
= arcsin( 0.1379 )
= 7° 55' 37"
(Tolkowsky rounds this off to 7° 52'.)
Ed. Note 4:
The critical angle is
arcsin(sin 90° / n)
= arcsin( 1 / 2.417)
= arcsin(0.4137)
= 24° 26' 23"
This 6 digit angle is absurdly precise,
because it is based on a number with only 4 digits (2.417).
The extra digits reduce the rounding errors
in further calculations in this article.
But all of the results should be rounded off.
(Tolkowsky rounds the critical angle off to 24° 26'.)
Note that this is valid for yellow sodium light.
Other colours have different indexes of refraction,
so they have different critical angles.
For example:
Index of Critical
Colour Refraction Angle Source Line Wavelength
Red 2.407 24° 33' Solar B-line 687 nm
Yellow 2.417 24° 26' Sodium D-line 589.3 nm
Violet 2.452 24° 4' Solar G-line 431 nm
The difference between the indexes of refraction (2.452 - 2.407) is the dispersion (0.044). (There is a small rounding error.)
The critical angles are calculated from the indexes of refraction.
All of the data besides the critical angles are taken from a GIA report:
Barak Green, Ilene Reinitz, Al Gilbertson, Mary Johnson, and James Shigley. "Diamond Optics Part 2: Light Dispersion, Color Wavelengths, and Fire." Gemological Institute of America, July 20, 2001. http://www.gia.org/giaresearch/diamond-cut5.cfm
Slightly different values are quoted by:
"Dana's System of Mineralogy."
7th Edition, Volume 1, page 148.
Ed. Note 5:
The average angle of incidence of the vertical rays is 0°,
just as Tolkowsky writes.
Ed. Note 6:
The average angle of incidence of the oblique rays is
i = 90° - arccos(2/3)
= 90° - 48° 11' 23"
= 41° 48' 37"
(Tolkowsky rounds this off to 42°.)
Ed. Note 7:
The corresponding angle of refraction is
r = arcsin(sin i / n)
= arcsin( 2/3 / 2.417 )
= arcsin( 0.2758 )
= 16° 0' 40"
(Tolkowsky rounds this off to 16°.)
Ed. Note 8:
The limiting angle of refraction of the oblique rays is
r = 90° - (180° - (90° - 24° 26' 23") - alpha)
= 90° - ( 90° + 24° 26' 23" - alpha)
= alpha - 24° 26' 23"
For alpha = 40° 45', this gives r = 16° 18' 37".
(Tolkowsky rounds this off to 16° 19').
Ed. Note 9:
The corresponding angle of incidence is
i = arcsin(n * sin r)
For r = 16° 18' 37", this gives i = 42° 44' 56".
(Tolkowsky rounds this off to 42½°.)
Ed. Note 10:
One-third of the light is incident from the right.
This light is incident from 19° 28' 16" to 90°.
[cos(90° - 19° 28' 16") - cos(90° - 90° )] / [cos(90° + 90°) - cos(90° - 90°)]
= [sin( 19° 28' 16") - sin( 90° )] / [sin( -90°) - sin( 90°)]
= [1/3 - 1] / [-1 - 1]
= [-2/3] / [-2]
= 1/3
Ed. Note 11:
Just part of the light incident from the right is effective.
This light is incident from 19° 28' 16"
to 42° 44' 56"
(actually an angle that depends on alpha).
[cos(90° - 19° 28' 16") - cos(90° - 42° 44' 56")] / [cos(90° + 90°) - cos(90° - 90°)]
= [sin( 19° 28' 16") - sin( 42° 44' 56")] / [sin( -90°) - sin( 90°)]
= [1/3 - 0.6788] / [-1 - 1]
= [-0.3455] / [-2]
= 0.1727
Ed. Note 12
So of the light incident from the right, only a fraction is effective:
0.1727 / (1/3)
= 0.5182
Actually, this fraction depends on alpha.
Editor's note 17
shows the formula used to calculate the values in Table III:
Table III
alpha fraction
39° 0.4114
40° 0.4725
40° 20' 0.4928
40° 45' 0.5182
41° 0.5334
42° 0.5938
(Tolkowsky rounds the fraction off to 0.493 .)
Ed. Note 13:
The crown angle is a weighted average of two angles shown in
fig. 35.
CrownAngle = ( FirstAngle * FirstWeight
+ SecondAngle * SecondWeight)
/ (FirstWeight + SecondWeight)
Ed. Note 14:
The first angle is between R'S' and the vertical.
FirstAngle = 180° - 4 * alpha.
(Tolkowsky rounds this to 17°.)
Ed. Note 15:
The weight given to the first angle is based on the area of the pavilion
directly underneath the table, because these rays entered the table
more or less vertically. Tolkowsky calculates the weight using TC * TC.
FirstWeight = TC * TC
TC = PM / cos alpha
= (DE / 2) * t / cos alpha
where t is the table ratio.
Note that the FirstWeight depends on both
the pavilion angle and the table ratio.
Ed. Note 16:
The second angle is between Q1R1 and the vertical.
It is also the angle between Q2E and the vertical,
as well as the angle between Q3R3 and the vertical.
SecondAngle = 2 * alpha - 12° 05'.
(Tolkowsky rounds this to 69½°.)
Editor's note 17 shows that the angle being subtracted (12° 05') depends on alpha.
Ed. Note 17:
The weight given to the second angle is based on the area of the pavilion
that reflects oblique rays to the crown facets, multiplied by the effective
fraction of the oblique rays. Tolkowsky writes that (SC * SC - Q2C * Q2C)
is proportional to the area.
SecondWeight = (SC * SC - Q2C * Q2C) * EffectiveFraction
The fraction was found in editor's note 12,
using this formula:
EffectiveAngle = arcsin(2.417 * sin (alpha - 24° 26' 23"))
EffectiveFraction = [cos(90° - 19° 28' 16") - cos(90° - EffectiveAngle)] / (-2) / (1/3)
= [sin( 19° 28' 16") - sin( EffectiveAngle)] / (-2) / (1/3)
= [1/3 - sin(EffectiveAngle)] * 3 / (-2)
In editor's note 16, the angle being subtracted depends on alpha.
The angle being subtracted is between the ray P2Q2 and the vertical.
This ray is incident at:
AverageEffectiveAngle = arcsin(( (1/3) + sin EffectiveAngle ) / 2)
This ray is refracted to follow P2Q2:
AverageRefractedAngle = arcsin((sin AverageEffectiveAngle) / 2.417)
= arcsin(( (1/3) + sin EffectiveAngle ) / 2 / 2.417)
For alpha = 40° 45', this gives angles of 30° 24' and 12° 5' respectively.
(Tolkowsky rounds them off to 30° 15' and 12° 0').
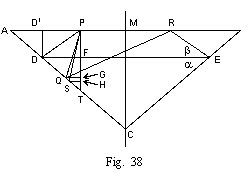
Ed. Note 18:
Fig. 38 is a simple version of fig. 35.
SC = ST + TC
Let point F be where the ray PT crosses the girdle DE.
Let point G be the point on the ray PT at the same height as Q.
Let point H be the point on the ray PT at the same height as S.
(QG and SH are perpendicular to PT).
Then,
TC = PM / cos alpha
SH = AP * (tan SPT) / (tan SPT + 1 / tan alpha)
SC = TC + SH / cos alpha
So we need to know AP and PM to find SC and TC.
Ed. Note 19:
Look at triangle PQR. Find PM in terms of QG.
PG = (QG + 2 * PM) * tan QRP
QG = PG * tan QPT
PG = QG / tan QPT
(QG + 2 * PM) * tan QRP = QG / tan QPT
2 * PM * tan QRP = QG * (1 / tan QPT - tan QRP)
PM = QG * (1 / tan QPT - tan QRP) / 2 / tan QRP
Let
g = (1 / tan QPT - tan QRP) / 2 / tan QRP
PM = QG * g
Ed. Note 20:
We know that ray PQ is reflected to QR,
so we can find angle QRP.
QRP = RQC - alpha
RQC = AQP
AQP = 90° - alpha + QPT
QRP = 90° - alpha + QPT - alpha
= 90° - 2 * alpha + QPT
Ed. Note 21:
Triangle PQT is split by QG. Find QG in terms of PT.
PT = PG + GT
GT = QG * tan alpha
PG = QG / tan QPT
PT = QG * tan alpha + QG / tan QPT
PT = QG * [tan alpha + (1 / tan QPT)]
QG = PT / [tan alpha + (1 / tan QPT)]
Ed. Note 22:
We also know PT in terms of AP.
PT = AP * tan alpha
Ed. Note 23:
Find AP in terms of QG.
QG = AP * tan alpha / [tan alpha + (1 / tan QPT)]
AP = QG * [tan alpha + (1 / tan QPT)] / tan alpha
Let
f = [tan alpha + (1 / tan QPT)] / tan alpha
f = 1 + (1 / tan QPT / tan alpha)
AP = QG * f
Ed. Note 24:
We now know both AP and PM in terms of QG, but QG is still unknown.
Use triangle ADP to find AP in terms of DE and PM.
In fig. 38, let D' be the point along AP directly above point D.
Then DD' is perpendicular to AP.
AP = AD' + D'P
DD' = D'P * tan beta
DD' = AD' * tan alpha
AD' * tan alpha = D'P * tan beta
AD' = D'P * tan beta / tan alpha
AP = AD' + D'P
= D'P * tan beta / tan alpha + D'P
= D'P * (1 + tan beta / tan alpha)
Let
h = 1 + tan beta / tan alpha
AP = D'P * h
D'P = DE / 2 - PM
AP = (DE / 2 - PM) * h
Ed. Note 25:
We can now combine the following equations to solve for QG:
AP = (DE / 2 - PM) * h
AP = QG * f
PM = QG * g
QG * f = (DE / 2 - PM) * h
QG * f = (DE / 2 - QG * g) * h
QG * (f + g * h) = DE / 2 * h
QG = DE / 2 * h / (f + g * h)
Ed. Note 26:
We can now solve for AP and PM in terms of DE.
This also gives the table ratio of a diamond with a knife edge girdle.
PM = DE / 2 * h / (f + g * h) * g
PM = DE / 2 * g * h / (f + g * h)
Let
t = g * h / (f + g * h)
PM = (DE / 2) * t
AP = QG * f
PM = QG * g
QG = PM / g
AP = PM * f / g
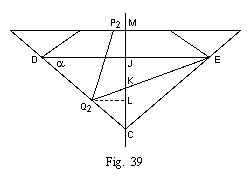
Ed. Note 27:
Fig. 39 is a simple version of fig. 35.
We will use ray Q2E to find Q2C.
Let point J be where the girdle DE crosses the axis MC.
Let point K be where ray Q2E crosses the axis MC.
Let point L be the point on the axis MC at the same height as Q2.
(Q2L is perpendicular to MC).
Then,
JC = JE * tan alpha
JK = JE * tan Q2ED
KL = Q2L * tan Q2ED
LC = Q2L * tan alpha
JC = JK + KL + LC
LC + KL = JC - JK
Q2L * (tan alpha + tan Q2ED) = JE * (tan alpha - tan Q2ED)
Q2L = JE * (tan alpha - tan Q2ED) / (tan alpha + tan Q2ED)
Q2C = Q2L / cos alpha
= JE / cos alpha * (tan alpha - tan Q2ED) / (tan alpha + tan Q2ED)
JE = (DE / 2)
Q2C = (DE / 2) / cos alpha * (tan alpha - tan Q2ED) / (tan alpha + tan Q2ED)
Ed. Note 28:
We can use line Q2KE to solve for angle Q2ED.
Angle Q2ED is between Q2E and the horizontal.
The SecondAngle is between Q2E and the vertical.
The AverageRefractedAngle is SPT
in figs. 35 and 38.
Q2ED = 90° - SecondAngle
SecondAngle = 2 * alpha - AverageRefractedAngle
Q2ED = 90° - 2 * alpha + AverageRefractedAngle
Ed. Note 29:
If the diamond has a culet,
part of the pavilion will be chopped off. How much is chopped off?
The culet is hard to measure accurately,
so there is no standard definition of how to measure it.
If we assume that the "culet" is:
culet = maximum diameter of the culet facet
If the culet is an octagon,
culet * cos(22° 30') = minimum diameter of the culet facet
Each side of the octagon crosses a pavilion main facet.
The midpoint of each side is on the centerline of the main facet.
The "culet height" is:
CuletHeight = (culet / 2) * cos(22° 30') * tan alpha
For alpha = 40° 45',
CuletHeight = (0.4) * culet
As of 2001, most diamond measuring machines measure the culet very inaccurately. For example, "pointed" or "no" culets are usually reported as 0.3% to 0.7% culets. It seems that these diamond measuring machines do NOT measure the culet itself. Instead, they measure other parameters, and do some math. Usually, the numbers do NOT add up. The machines attribute the error to the culet.
If you have a better explanation of the culet, please let me know.
Ed. Note 30:
The formulas derived above are summarized in
editor's note 36.
Unfortunately, not all of the proportions that satisfy these formulas
result in ideal diamonds. Two problems are fish-eye diamonds
and nail-head diamonds.
Editor's notes 30-32 are based on the explanation of fish-eyes
in the PriceScope
fish-eye tutorial.
Fish-eye diamonds occur when the pavilion angle is small enough to break one of Tolkowsky's assumptions. Tolkowsky assumes that the rays that enter the table vertically are doubly reflected before exiting the crown.
If the reflection of PT ends up higher than the girdle,
then a reflection of the girdle will appear in the table.
If the girdle is unfinished, this reflection looks like a gigantic inclusion.
Pictures of fish-eye diamonds are available at:
http://www.pricescope.com/tutor_fisheye.asp
Ed. Note 31:
We can use the reflection of PT to guess whether a diamond will have a fish-eye.
The reflection of PT has an inclination of:
= 90° - 2 * alpha
The reflection's slope is:
= tan(90° - 2 * alpha)
Point T is beneath the girdle, by this much:
= diameter / 2 * (1 - t) * tan alpha
Point T is to the left of point E, by this much:
= diameter / 2 * (1 + t)
So we have fish eye if:
diameter / 2 * (1 + t) * tan(90° - 2 * alpha)
> diameter / 2 * (1 - t) * tan alpha
(1 + t) * tan(90° - 2 * alpha)
>
(1 - t) * tan alpha
Of course, we need to adjust for the girdle thickness.
Also, if the diamond is tilted, we need to use a different ray
instead of PT. But we can guess whether the diamond will have a fish-eye,
even if we don't make these adjustments.
Ed. Note 32:
A diamond with:
alpha = 38° 15',
beta = 39° 14',
t = 0.532
satisfies the equations in editor's note 36,
but is on the verge of being a fish-eye.
These two solutions have been removed from
Table IV (in editor's note 37):
Pavilion Crown Table
Angle Angle Ratio Total Height Ratio
(alpha) (beta) (t)
37° 40° 56' 0.528 0.581 - culet height fish-eye
38° 39° 35' 0.531 0.584 - culet height fish-eye
Ed. Note 33:
A nail-head occurs when the person looking at the diamond
sees the reflection of their own head.
It is caused by pavilion and lower girdle facet angles close to 45°.
Michael Cowing has published a picture of a nail-head diamond with:
alpha = 42° 36',
beta = 30°,
t = 0.69
The diamond is pictured in Figure 9, and described in Table I, of:
Michael Cowing. "Diamond brilliance: theories, measurement, and judgement." Journal of Gemmology. Volume 27, Number 4, October 2000, pages 209-227. Copyright by the Gemmological Association and Gem Testing Laboratory of Great Britain.Cowing has posted an Adobe Acrobat version of this article at: http://www.geocities.com/acagemlab/ He apologizes "for the poor picture quality and ad popups. It is a free site."
Ed. Note 34:
A diamond with:
alpha = 42° 36',
beta = 29° 30',
t = 0.537
satisfies Tolkowsky's model. This diamond is very similar
(in terms of crown angle and pavilion angle) to the nail-head diamond
in Cowing's article.
These two solutions have been removed from
Table IV:
Pavilion Crown Table
Angle Angle Ratio Total Height Ratio
(alpha) (beta) (t)
43° 27° 40' 0.535 0.588 - culet height nail-head
44° 20° 30' 0.52 0.572 - culet height nail-head
Also, this solution (still in
Table IV) is questionable:
42° 31° 41' 0.539 0.593 - culet height
If you have evidence that these parameters do not result in a good diamond,
please let me know.
Ed. Note 35:
Tolkowsky mentions the girdle. He even says that the diamond is circular.
But he does not include the thickness of the girdle in the overall depth of the diamond.
To finish the diamond design, we need to estimate the thickness of the girdle.
I have written an article titled,
"Diamond Girdles --
How Adding a Girdle Changes Marcel Tolkowsky's Diamond Design."
The article uses the same logic as Tolkowsky, and most of the same formulas,
but adds in the girdle. For any given pavilion angle,
the girdle increases the optimum table ratio,
and reduces the optimum crown angle. The article
is posted at:
http://www.folds.net/diamond_girdle/index.html
Ed. Note 36:
These formulas are the same as Tolkowsky's geometric model.
They were derived in the editor's notes (above).
These formulas start with a pavilion angle (alpha)
and a guess at the crown angle (beta).
Then we need to loop through the formulas a few times
to find the best crown angle and table ratio
for the pavilion angle.
Then we will need to make sure that the diamond really is pretty.
Editor's notes 30-34 explain that some combinations
of proportions that satisfy this model make
fish-eye or
nail-head diamonds,
which are NOT ideal. And of course, the only way to judge
if the diamond really is beautiful is to look at it in appropriate light.
Caution: These formulas use the same assumptions and logic as Tolkowsky -- including a knife-edge girdle. Formulas that include typical girdles are available in an article at: http://www.folds.net/diamond_girdle/index.html
Start.
We choose alpha.
We start with a guess for beta (say, 35°).
Step 1. We look at the girdle:
DE = diameter of a knife-edge diamond. (1 mm is easiest.)
Step 2. We find out what fraction of the oblique rays are effective, and their average angle:
CriticalAngle = arcsin(1 / 2.417) = 24° 26' 23"
EffectiveAngle = arcsin(sin (alpha - 24° 26' 23") * 2.417)
EffectiveFraction = [1/3 - sin(EffectiveAngle)] * 3 / (-2)
SPT = AverageRefractedAngle = arcsin(( (1/3) + sin(EffectiveAngle) ) / 2 / 2.417)
Step 3. We calculate angles of rays:
QPT = alpha - 24° 26' 23"
QRP = 90° - 2 * alpha + QPT
Q2ED = 90° - 2 * alpha + AverageRefractedAngle
Step 4. We calculate angles of typical rays before they leave the crown.
The FirstAngle is the angle between R'S' and the vertical.
The SecondAngle is the angle between Q1R1 and the vertical.
FirstAngle = 180° - 4 * alpha
SecondAngle = 2 * alpha - AverageRefractedAngle
Step 5. We calculate some ratios that make the calculations easier.
f = 1 + (1 / tan QPT / tan alpha)
g = (1 / tan QPT - tan QRP) / 2 / tan QRP
Step 6. The loop starts here.
We calculate the table ratio of a knife-edge diamond:
h = 1 + tan beta / tan alpha
t = g * h / (f + g * h)
Step 7. We calculate distances at the top of the diamond:
PM = (DE / 2) * t
AP = PM * f / g
Step 8. We calculate distances along the pavilion edge:
TC = PM / cos alpha
SC = TC + AP * (tan SPT) / (tan SPT + 1 / tan alpha) / cos alpha
Q2C = (DE / 2) / cos alpha * (tan alpha - tan Q2ED) / (tan alpha + tan Q2ED)
Step 9. We calculate a new guess for beta (the crown angle).
FirstWeight = (TC * TC)
SecondWeight = EffectiveFraction *
(SC * SC - Q2C * Q2C)
beta = (FirstWeight * FirstAngle + SecondWeight * SecondAngle)
/ (FirstWeight + SecondWeight)
This gives us a new guess for beta.
The loop ends here.
We can repeat steps 6-9 until the guess for beta stops changing.
Step 10. Because Tolkowsky uses a knife-edge girdle,
we do NOT need to adjust the diameter and table ratio.
Step 11. Tolkowsky says that:
Modern diamonds have longer lower girdle facets, so these angles are slightly different.
Step 12. The diamond total depth contains the crown and the pavilion.
Because it has a knife-edge girdle, there is no girdle thickness:
CrownHeight = diameter / 2 * (1 - t) * tan beta
PavilionDepth = diameter / 2 * tan alpha
-(CuletHeight) =-((culet / 2) * cos(22° 30') * tan alpha)
TotalDepth = CrownHeight + PavilionDepth - CuletHeight
Ed. Note 37 / Table IV:
Here are some combinations of alpha, beta, and t calculated by this method.
The total depth ratio is also shown. The total depth ratio
is the overall depth of the diamond divided by the diameter.
It includes an adjustment for the culet facet,
but not for the knife-edge girdle.
Pavilion Crown Table
Angle Angle Ratio Total Depth Ratio
(alpha) (beta) (t)
39° 38° 9' 0.534 0.588 - culet height
40° 36° 30' 0.537 0.591 - culet height
40° 45' 35° 1' 0.539 0.593 - culet height
41° 34° 27' 0.539 0.593 - culet height
42° 31° 41' 0.539 0.593 - culet height
Caution: The model breaks down at both ends of this range.
Editor's notes 30-34
show that some diamonds that match the formulas are NOT ideal.
Extrapolating to smaller pavilion angles makes
fish-eyes.
Extrapolating to larger pavilion angles makes
nail-heads.
If you have evidence that a row of parameters (in this table)
describes poor diamonds,
please let me know.
Caution: These results use the same assumptions and logic as Tolkowsky -- including a knife-edge girdle. Formulas that include typical girdles are available in an article at: http://www.folds.net/diamond_girdle/index.html
FOLDS.NET has software that lets you adjust fig. 35. You can see the effect of changing the pavilion angle or the girdle thickness. You can view the calculations, or just look at the results.
The MSU diamond study found similar results, with some noticeable differences.
The MSU diamond study was much more thorough than this model.
Ed. Note 38:
As shown in Table II,
Tolkowsky's rounding errors are small, but noticeable.
Editor's note 37 shows that for a pavilion angle of 40° 45',
the best crown angle is 35°, with a table ratio of 0.54 .
Tolkowsky's various rounding errors cause him to estimate
that for a pavilion angle of 40° 45',
the best crown angle is 34° 30', with a table ratio of 0.53 .
Notably, these errors do not change the crown height.
Also, these errors partly offset the error from not including the girdle thickness.
Tolkowsky does not include the thickness of the girdle. The girdle adds considerable thickness -- because of both the nominal "girdle" thickness, and because of the waviness of the girdle. The waviness is about 1.7% of the diamond's diameter. Formulas that include typical girdles are available in an article at: http://www.folds.net/diamond_girdle/index.html
This model assumes a pointed culet.
Ed. Note 39:
Tolkowsky's model does not follow all of the rays that strike the diamond.
It emphasizes rays that enter through the table, which are about 28% of the total.
It pays less attention to rays that enter or exit through the star facets, upper girdle facets, and lower girdle facets. It does not explain if (or how) changing the pavilion angle should change the slopes of these facets.
It assumes that all rays that exit the bottom of the diamond are lost. It assumes that either no rays enter the bottom of the diamond, or that they do not make it out the top of the diamond.
Tolkowsky does not consider how the thickness of the girdle changes the paths of the light. In reality, the optimum crown angle and table ratio are functions of both the pavilion angle and the girdle thickness. Formulas that include typical girdles are available in an article at: http://www.folds.net/diamond_girdle/index.html
It is not a 3-D model. It only follows rays that bounce around in a single plane. Although very few rays only bounce around in a single plane, these rays provide a good average for the behavior of the rays that cross them in all directions.
Ed. Note 40:
Tolkowsky studies brilliance and fire,
but not scintillation.
Tolkowsky gives brilliance and fire equal weight,
by multiplying them together.
Ed. Note 41:
A computer performed the calculations in this appendix.
Jasper Paulsen (the editor of this book) created the software, and posted it at FOLDS.NET.
You can use "Diamond Cross-Section" to adjust fig. 35.
You can see the effect of changing the pavilion angle
or the girdle thickness. You can view the calculations,
or just look at the results.
FOLDS.NET also has software for calculating the lengths of all of the edges
of a perfectly symmetrical diamond. The software is available at:
http://www.folds.net/diamond
This software can be used to calculate other combinations of proportions that also satisfy Tolkowsky's model. Unfortunately, some of these proportions do not result in ideal diamonds. Two problems are fish-eye diamonds and nail-head diamonds.
Ed. Note 42:
Sergey Sivovolenko (of OctoNus Software),
Yurii Shelementiev (of the Gemology center of Moscow State University),
and Anton Vasiliev (of the LAL company)
have created a 3-D model of a diamond.
Just like Tolkowsky, they gave brilliance and fire equal weight
by multiplying them together.
They found a similar relationship between optimum crown angle
and actual pavilion angle.
(Their simulations suggest slightly smaller pavilion angles.
The difference is about the same as Tolkowsky's rounding error.)
Their report is available at
http://www.gemology.ru.
The following pages show the relationship particularly clearly:
Ed. Note 43:
The Gemological Institute of America
has extensively studied diamond cut
(http://www.gia.org/giaresearch/diamond-cut3.cfm).
The GIA has created another 3-D model of a diamond.
They do not report as clear a relationship between optimum crown angle
and actual pavilion angle. A summary of their report is available
in the May 1999 edition of Canadian Jeweller:
http://canjewel.polygon.net/docs/may99/cut.html.
Garry Holloway has interpreted the GIA data at: http://www.diamond-cut.com.au/04_previous.htm (Holloway's web-site uses JavaScript menus.)
Ed. Note 44:
Garry Holloway
has studied the effects of many facet proportions on
diamond beauty. He conducted these studies using MSU and Octonus
'DiamCalc' software and actual diamonds.
Leonid Tcharnyi wrote a computer program that uses
Holloway's data. The program produces a numerical score (HCA) and written
descriptions of a round brilliant cut diamond.
A detailed explanation of the "Holloway Cut Advisor"
is available at: http://www.diamond-cut.com.au/
(Holloway's web-site uses JavaScript menus.)
A web service that uses this software is available at:
http://www.pricescope.com/cutadviser.asp
Ed. Note 45:
In the real world, extremely well cut diamonds are rare.
Of course, it is almost impossible to make every diamond
match just a single set of parameters.
But even if one includes diamonds close to the optimum ranges
in this study, the MSU study, and the GIA study,
very few diamonds are extremely well cut.
In order to purchase a diamond that is extremely well cut, a buyer will need to make trade-offs of cut parameters, symmetry, polish, colour, fluorescence, size of crystal defects (clarity), carat weight, cost, and availability.
Three on-line databases that show the economic trade-offs among these features are:
Acknowledgements: I thank the late Marcel Tolkowsky for writing Diamond Design. I thank everyone kind enough to criticize this web-site, and tell me things that I should fix. Garry Holloway, Marvin Leib, Bruce Harding, Martin Haske, Michael Cowing, Jefferson Lewis, Thomas Kabele, Iiro Suokko, and the Gemological Institute of America (GIA) have pointed out errors and omissions. If you notice one, please let me know, and I will do my best to fix it promptly.
NOTE: This information and software are for educational purposes only and should not be used in place of services from a professional appraiser. Formulas cannot be 100% accurate due to subtleties not included in the formulas. All decisions should be based on your own knowledge. I cannot accept any responsibility for decisions you make.
Thank you for visiting
FOLDS.NET.
The first edition was published in 1919 by Marcel Tolkowsky in the United States and the United Kingdom.
Web formatting, transcription, figures 38 and 39, and editor's notes are
copyright 1995-96, 2001-02 by
Jasper Paulsen.
Your comments are welcomed.
Begun August 2001. First posted September 15, 2001.
Last updated November 15, 2003.